Graphs represent relationships between entities, and visualizing these relationships effectively is crucial for understanding the underlying data. Traditional graph drawing algorithms often focus on optimizing single readability criteria—such as minimizing edge crossings or preserving distances—while neglecting others. To overcome this limitation, we propose a novel graph layout approach that emphasizes vertex resolution using circumcircles.

Vertex Resolution Using Circumcircles:

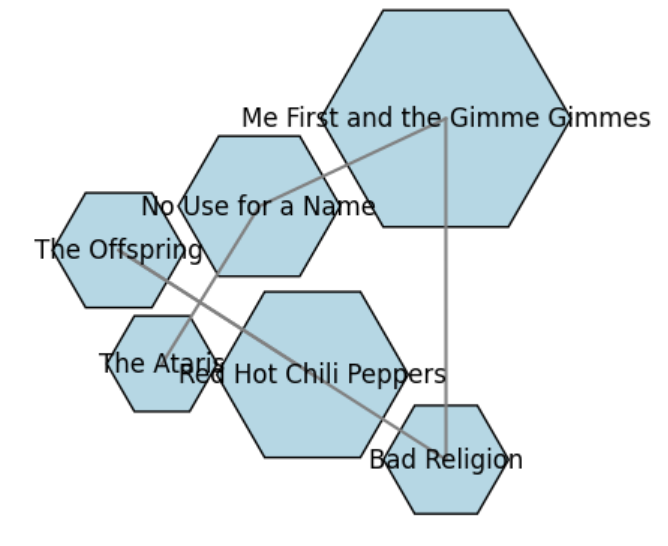
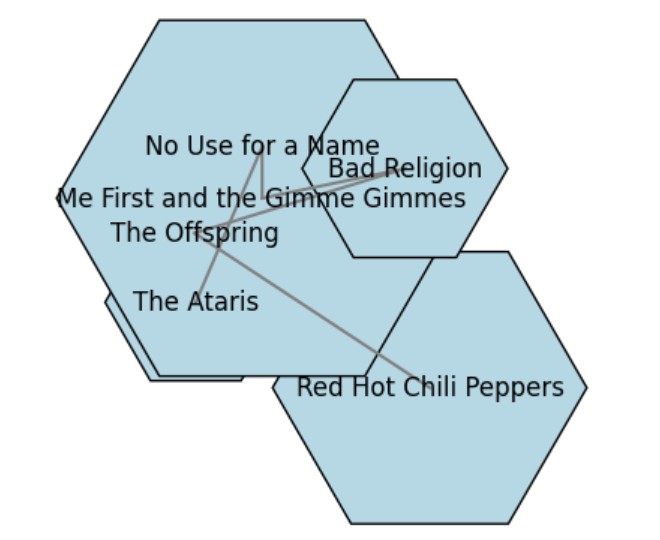
Vertex resolution is a key readability criterion that ensures nodes in a graph are distinguishable and well-separated. Our approach introduces the concept of circumcircles to enhance vertex resolution. Each node is enclosed within a circumcircle, and the size of the circumcircle is determined by the length of the node’s label. By optimizing the positions of the nodes, we ensure that the circumcircles do not overlap, thereby improving the overall readability of the graph.

Key Features:

Circumcircle-Based Vertex Resolution:

Each node is enclosed within a circumcircle. The radius of the circumcircle is proportional to the length of the node’s label, ensuring that larger labels have more space. Nodes are positioned such that their circumcircles do not overlap, enhancing the clarity and separation between nodes.

Multi-Criteria Optimization:

Our approach can optimize multiple readability criteria simultaneously, including ideal edge lengths, stress (distance preservation), neighborhood preservation, vertex resolution, angular resolution, and aspect ratio. This ensures a balanced approach to graph readability, where no single criterion is prioritized at the expense of others.

Gradient Descent for Optimization:

The positions of the nodes are optimized using gradient descent, a powerful method that iteratively adjusts the node positions to minimize the overlap between circumcircles and improve other readability criteria. By combining smooth and non-smooth functions, our approach can handle complex criteria that are difficult to optimize using traditional methods.

Effectiveness:

This is a both quantitative and qualitative evidence of the effectiveness of our approach through 
experimental data and a functional prototype. By incorporating vertex resolution using circumcircles, 
our method ensures that nodes are well-separated and readable, even in dense graph layouts. This 
enhances the overall comprehension of the graph, making it easier to understand the relationships 
between entities.